Answer: (-8,-7) is the center of circle with radius 4 units
Explanation:
Given equation :
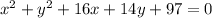
We have to find the center and radius of the circle
As we know the equation of circle is of the form
 where (h,k) is center and r is radius
where (h,k) is center and r is radius
So we have
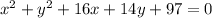
Using completing the square method
![x^2+16x+y^2+14y+97=0\\\\\Rightarrow x^2+16x+64-64+y^2+14y+49-49+97=0\\\\\Righatrrow (x^2+16x+64)+(y^2+14y+49)-49-64+97=0\\\\\Righatrrow (x+8)^2+(y+7)^2-16=0 \text { }[{\because}(a+b)^2=a^2+b^2+2ab ]\\\\\Righatrrow (x+8)^2+(y+7)^2=16\\\\\Righatrrow (x+8)^2+(y+7)^2=4^2](https://img.qammunity.org/2021/formulas/mathematics/middle-school/s0imxed2zeqq4yl8digkd3qpjggqtgf78w.png)
Comparing to the equation of circle we get
h = -8 , k = -7 and r = 4
Hence, (-8,-7) is the center of circle with radius 4 units