Question

A 10.0-g bullet is fired into a stationary block of wood having mass 5.00 kg. The bullet embeds 10 pts into the block and the speed of the block-and-bullet after the collision is 0.600 m/s. Find a) the original speed of the bullet, b) the mechanical energies of the block-bullet system before and after the collision, c) the percentage of mechanical energy lost to heat.

Answer 1

A. The initial velocity of the bullet is
`= 300.6m/s`

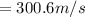
B. Mechanical energy of the system before and after collision: 451.80 J, 0.9018 J

C. Percentage of K.E lost to heat is = 99.8 %

Step-by-step explanation:

From conservation of linear momentum,

`(m_(1)v_(1) +m_(2)v_(2))= (m_(1)+m_(2))v`

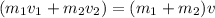
let the mass of the block be m1 and velocity = v1

let the mass of the bullet be m2 and velocity = v2

Let the final velocity of the system be v.

A. Plugging our parameters into the equation, we have:

`[(5 * 0) +(0.01* v_(2))]= 5.01 * 0.6`

`v_(2)=(3.006)/(0.01)= 300.6m/s`

Hence, the initial velocity of the bullet is
`= 300.6m/s`

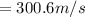
B. The mechanical energies of the system exist in form of kinetic energy.

I. Kinetic energy of the system before collision:

`0.5 * 5* 0^(2) + 0.5 * 0.01 * 300.6^(2)= 451.80 J`

II. Kinetic energy after collision:

`0.5* 5.01 * 0.6^(2)= 0.9018 J`

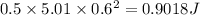
C. Change in Mechanical Energy =
`451.8 - 0.9018 J= 450.9J`

`(450.9)/(451.8) * 100 =99.8%`

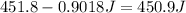
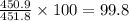
Percentage of K.E lost to heat is = 99.8 %