Answer:
A. The initial velocity of the bullet is
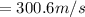
B. Mechanical energy of the system before and after collision: 451.80 J, 0.9018 J
C. Percentage of K.E lost to heat is = 99.8 %
Step-by-step explanation:
From conservation of linear momentum,
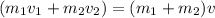
let the mass of the block be m1 and velocity = v1
let the mass of the bullet be m2 and velocity = v2
Let the final velocity of the system be v.
A. Plugging our parameters into the equation, we have:
![[(5 * 0) +(0.01* v_(2))]= 5.01 * 0.6](https://img.qammunity.org/2021/formulas/physics/college/lw4uo5oozjohbfcezasyp5u9um1p8yc21h.png)
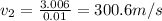
Hence, the initial velocity of the bullet is
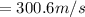
B. The mechanical energies of the system exist in form of kinetic energy.
I. Kinetic energy of the system before collision:
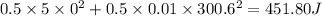
II. Kinetic energy after collision:
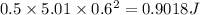
C. Change in Mechanical Energy =
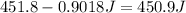
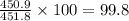
Percentage of K.E lost to heat is = 99.8 %