Question

What interval includes all possible values of x, where -306 - 2x) > 4x + 12?

Answer 1

Corrected Question

What interval includes all possible values of x, where –3(6 – 2x) ≥ 4x + 12?

A. (–∞, –3] (B) [–3, ∞) (C)(–∞, 15] (D)[15, ∞)

Answer:

(D)[15, ∞)

Explanation:

We want to determine what interval of x includes all possible values of x in:
`-3(6 - 2x) \geq 4x + 12`

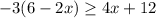
First, we open the bracket on the Left hand side

`-18+6x \geq 4x + 12`

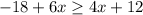
Next, we collect terms with x on the Left hand side and constants on the right hand side.

`6x-4x \geq 12+18\\2x\geq 30\\$Divide both sides by 2\\x \geq 15`

Therefore, the interval of x which includes all possible values of x is [15, ∞).

Option D is the correct option.