Corrected Question
What interval includes all possible values of x, where –3(6 – 2x) ≥ 4x + 12?
A. (–∞, –3] (B) [–3, ∞) (C)(–∞, 15] (D)[15, ∞)
Answer:
(D)[15, ∞)
Explanation:
We want to determine what interval of x includes all possible values of x in:
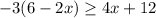
First, we open the bracket on the Left hand side
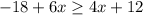
Next, we collect terms with x on the Left hand side and constants on the right hand side.
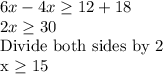
Therefore, the interval of x which includes all possible values of x is [15, ∞).
Option D is the correct option.