Question

A lab technician made a 14 cm diameter hole through the middle of a cylinder that has a diameter of 20 cm and a height of 28 cm. What is the approximate volume of the finished cylinder, to the nearest tenth of a centimeter

Answer 1

The volume of the finished cylinder is
`4486.2 m^3`

Explanation:

To find the volume of the finished cylinder, we have to first find the volume of the hole (with 14 cm diameter and a height of 28 cm) and subtract it from the volume of the original cylinder (with diameter of 20 cm and a height of 28 cm).

Note: The hole is also cylindrical in shape.

The volume of a cylinder is given as:

`V = \pi r^2h`

where r = radius, h = height

VOLUME OF THE HOLE

The diameter of the hole is 14 cm, hence, its radius is 7 cm (14 / 2 = 7)

Its volume is:

`V = \pi *7^2 * 28\\V = 4310.3 m^3`

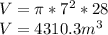
VOLUME OF THE ORIGINAL CYLINDER

The diameter of the cylinder is 20 cm, hence, its radius is 10 cm (20 / 2 = 10)

Its volume is:

`V = \pi *10^2 * 28\\V = 8796.5 m^3`

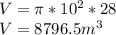
Hence, the volume of the finished cylinder will be:

`8796.5 - 4310.3 = 4486.2 m^3`

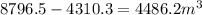
The volume of the finished cylinder is
`4486.2 m^3`