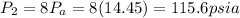Answer:
Pressure = 115.6 psia
Step-by-step explanation:
Given:
v=800ft/s
Air temperature = 10 psia
Air pressure = 20F
Compression pressure ratio = 8
temperature at turbine inlet = 2200F
Conversion:
1 Btu =775.5 ft lbf,
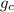 = 32.2 lbm.ft/lbf.s², 1Btu/lbm=25037ft²/s²
= 32.2 lbm.ft/lbf.s², 1Btu/lbm=25037ft²/s²
Air standard assumptions:
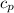 = 0.0240Btu/lbm.°R, R = 53.34ft.lbf/lbm.°R = 1717.5ft²/s².°R 0.0686Btu/lbm.°R
= 0.0240Btu/lbm.°R, R = 53.34ft.lbf/lbm.°R = 1717.5ft²/s².°R 0.0686Btu/lbm.°R
k= 1.4
Energy balance:
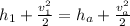
As enthalpy exerts more influence than the kinetic energy inside the engine, kinetic energy of the fluid inside the engine is negligible
hence

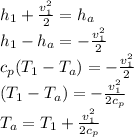
 = 20+460 = 480°R
= 20+460 = 480°R
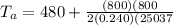 = 533.25°R
= 533.25°R
Pressure at the inlet of compressor at isentropic condition
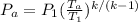
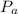 =
=
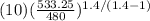 = 14.45 psia
= 14.45 psia