Question

A survey was taken of randomly selected​ Americans, age 65 and​ older, which found that 401 of 1020 men and 536 of 1059 women suffered from some form of arthritis. ​a) Are the assumptions and conditions necessary for inference​ satisfied? Explain. ​b) Create a​ 95% confidence interval for the difference in the proportions of senior men and women who have this disease. ​c) Interpret your interval in this context. ​d) Does this suggest that arthritis is more likely to afflict women than​ men? Explain.

Answer 1

The assumptions and conditions necessary for inference are satisfied, and a 95% confidence interval can be created to estimate the difference in proportions of senior men and women with arthritis. The interval provides a measure of precision, and the results do not suggest that arthritis is more likely to afflict women than men.

Step-by-step explanation:

a) The assumptions and conditions necessary for inference are satisfied. Random sampling was used to select Americans age 65 and older, which helps ensure representativeness. The sample sizes are also large enough for accurate analysis.

b) To create a 95% confidence interval for the difference in proportions, we can use the formula:
CI = (p1 - p2) ± Z * sqrt((p1(1-p1)/n1) + (p2(1-p2)/n2))

c) The 95% confidence interval indicates that we are 95% confident that the true difference in proportions falls within the given range. It provides a measure of the precision of our estimate.

d) The survey results do not suggest that arthritis is more likely to afflict women than men. The confidence interval encompasses a range of values, indicating that the difference in proportions could be quite small or even favor men.

Answer 2

a) yes The assumptions and conditions necessary for inference.

b)The 95% of confidence intervals for p₁-p₂ is determined by

(-0.15523,-0.07057)

c) The sample proportion of men = 0.3931 = 39%

The sample proportion of women = 0.5061 = 50%

we observe that arthritis is more likely to afflict women than​ men

Step-by-step explanation:

Explanation:-

a) yes The assumptions and conditions necessary for inference.

b)

Given A survey was taken of randomly selected​ Americans, age 65 and​ older, which found that 401 of 1020 men suffered from some form of arthritis.

Given first sample size 'n₁' = 1020

First sample proportion

'p₁' =
`(x)/(n) = (401)/(1020) = 0.3931`

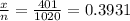
q₁ = 1-p₁ = 1-0.3931 =0.6069

Given A survey was taken of randomly selected​ Americans, age 65 and​ older, which found that 536 of 1059 men suffered from some form of arthritis

Given second sample size 'n₂' = 1059

Second sample proportion

`p_(2) = (x)/(n) = (536)/(1059) = 0.5061`

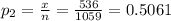
q = 1-p =1-0.5061 =0.4939

Step(ii):-

The 95% of confidence intervals for p₁-p₂ is determined by

`[p_(1) - p_(2) - Z_(\alpha ) S.E(p_(1) - p_(2)) ,p_(1) - p_(2) + Z_(\alpha ) S.E(p_(1) - p_(2))]`

where

`S.E (p_(1) -p_(2) ) =\sqrt{(p_(1) q_(1) )/(n_(1) ) +(p_(2) q_(2) )/(n_(2) ) }`

`S.E (p_(1) -p_(2) ) =\sqrt{(0.3931 X0.6069 )/(1020 ) +(0.506X0.494 )/(1059) }`

`S.E (p_(1) -p_(2) ) = √(0.0004699)`

`S.E (p_(1) -p_(2) ) = 0.0216`

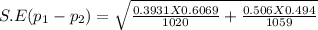
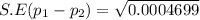
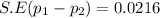
Step(iii):-

The 95% of confidence intervals for p₁-p₂ is determined by

`[p_(1) - p_(2) - Z_(\alpha ) S.E(p_(1) - p_(2)) ,p_(1) - p_(2) + Z_(\alpha ) S.E(p_(1) - p_(2))]`

(0.3931-0.506 - 1.96 ×0.0216 , 0.3931-0.506 +1.96 ×0.0216)

(-0.1129-0.04233, -0.1129+0.04233)

(-0.15523,-0.07057)

Final answer:-

95% confidence interval for the difference in the proportions of senior men and women who have this disease.

(-0.15523,-0.07057)

c)

The sample proportion of men = 0.3931 = 39%

The sample proportion of women = 0.5061 = 50%

we observe that arthritis is more likely to afflict women than​ men