What is the equation of the line that passes through the points (2,3) and (6,5)

Question

asked Oct 26, 2023 198k views

1 Answer

Craymichael · Answer 1 · 2023-10-31T18:09:29+0000

Answer:

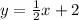
y=(1)/(2)x+2

Explanation:

We can find the slope by using the formula

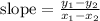$\text{slope}=(y_1-y_2)/(x_1-x_2)$ .

Plugging in the points (2,3) and (6,5), we have

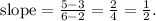
$\text{slope}=(5-3)/(6-2)=(2)/(4)=(1)/(2).$

Therefore, the slope is
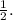(1)/(2). We can then write the line in slope-intercept form, which is
y=mx+b where
is the slope and
is the y-intercept.

We already found the slope, so we know the equation is of the form

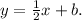
y=(1)/(2)x+b.

We can now plug in either one of the points to find
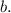Plugging in (2,3), we get

3=(1)/(2)(2)+b .

To solve for
, we can subtract 1 from both sides of the equation:

3=1+b

b=3-1=2 .

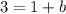
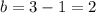Now, we have all the variables we need to write the equation in slope-intercept form. We know
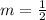m=(1)/(2) and
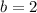b=2 , so the equation is

y=(1)/(2)x+2.