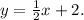Answer:
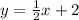
Explanation:
We can find the slope by using the formula
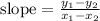 .
.
Plugging in the points (2,3) and (6,5), we have
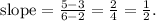
Therefore, the slope is
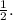 We can then write the line in slope-intercept form, which is
We can then write the line in slope-intercept form, which is
 where
where
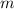 is the slope and
is the slope and
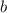 is the y-intercept.
is the y-intercept.
We already found the slope, so we know the equation is of the form
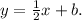
We can now plug in either one of the points to find
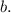 Plugging in (2,3), we get
Plugging in (2,3), we get
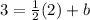 .
.
To solve for
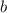 , we can subtract 1 from both sides of the equation:
, we can subtract 1 from both sides of the equation:
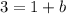
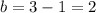 .
.
Now, we have all the variables we need to write the equation in slope-intercept form. We know
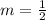 and
and
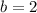 , so the equation is
, so the equation is