Answer:
(a) Is not possible
(b) It is possible
(c) It is possible
(d) Is NOT possible.
Explanation:
(a)
Is not possible, notice that for any function
 such that
such that
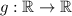
you would have that
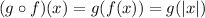
And for, lets say -3,3 you have that
 therefore is not possible to find a function that is one to one.
therefore is not possible to find a function that is one to one.
(b)
It is possible. Take the following function
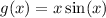 since
since
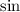 is periodic it will take positive and negative numbers and if you multiply by
is periodic it will take positive and negative numbers and if you multiply by
 each period will become bigger and bigger.
each period will become bigger and bigger.
(c)
It is possible. Take the function

Then
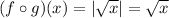 and
and
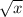 is one to one.
is one to one.
(d)
It is NOT possible because
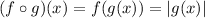 and that will always be positive.
and that will always be positive.