Question

Two new drugs are to be tested using a group of 60 laboratory mice, each tagged with a number for identification purposes. Drug A is to be given to 22 mice, drug B is to be given to another 22 mice, and the remaining 16 mice are to be used as controls. How many ways can the assignment of treatments to mice be made? (A single assignment involves specifying the treatment for each mouse—whether drug A, drug B, or no drug.)

Answer 1

The total number of ways of assignment is 314,790,828,599,338,321,972,833,000.

Explanation:

In mathematics, the procedure to select k items from n distinct items, without replacement, is known as combinations.

The formula to compute the combinations of k items from n is given by the formula:

`{n\choose k}=(n!)/(k!(n-k)!)`

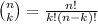
In this case we need to determine the number of ways in which the drugs are assigned to each mouse.

It is provided that new drugs are to be tested using a group of 60 laboratory mice, each tagged with a number for identification purposes.

Drug A is to be given to 22 mice.

Compute the number of ways to assign drug A to 22 mice as follows:

`{60\choose 22}=(60!)/(22!(60-22)!)\\\\=(60!)/(22!* 38!)\\\\=14154280149473100`

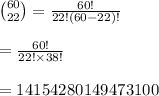
Now the remaining number if mice are: 60 - 22 = 38.

Compute the number of ways to assign drug B to 22 mice as follows:

`{38\choose 22}=(38!)/(38!(38-22)!)\\\\=(38!)/(22!* 16!)\\\\=22239974430`

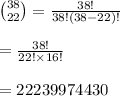
Now the remaining number if mice are: 38 - 22 = 16.

Compute the number of ways to assign no drug to 16 mice as follows:

`{16\choose 16}=(16!)/(16!(16-16)!)\\\\=1`

The total number of ways of assignment is:

`N = {60\choose 22}* {38\choose 22}* {16\choose 16}\\\\=14154280149473100* 22239974430* 1\\\\=314,790,828,599,338,321,972,833,000`

Thus, the total number of ways of assignment is 314,790,828,599,338,321,972,833,000.