Question

Answer the following questions about the problem above. Write in complete sentences to get full credit.

1. What is the slope for section "b" of Mrs. Washington's commute.

2. What is the slope for section "c" of Mrs Washington's commute?

3. Explain the difference in "b" and "c" in context of Mrs. Washing driving home.

4. How far does Mrs. Washington live from her work?

Answer 1

1. Speed = 1 mph

2. ¼ mph

3. She's driving at 4 times faster speed in b than c

4. 20 miles

Explanation:

1. Slope of a distance time graph is the speed

(15-7)/(16-8)

8/8

1 mph

2. Speed = (7-6)/(20-16)

1/4 mph

3. Speed in b is greater than c

1 = 4(¼)

4. Distance from 20 to 0, is 20 miles

Answer 2

1. -1

2. -1/4

3. As the line nears closer to y = 0, Mrs. Washington is getting closer to her house. As such, the line represents miles driven per minute, representing speed. As the slope of the line becomes steeper, as it does during section B of the commute, Mrs. Washington is driving one mile per minute, or 60 miles per hour. As she drives through section C, she only drove 1 mile after 4 minutes, or 15 miles per hour.

4. She lives 20 miles from her office.

Explanation:

1. You can find the slope for section B of the commute by taking two points in section B and using them to find the slope.

I will take (10, 13) and (14, 9) as my points.

You can use
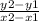`(y2-y1)/(x2-x1)` to find the slope:

`(13-9)/(10-14) \\\\(4)/(-4)`

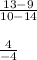
The slope for section b is -1.

2. You can find the slope for section C using the same method.

I will use the points (16, 7) and (20, 6):

`(7-6)/(16-20) \\\\(1)/(-4)`

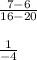
The slope for section c is -1/4.

3. As the line nears closer to y = 0, Mrs. Washington is getting closer to her house. As such, the line represents miles driven per minute, representing speed. As the slope of the line becomes steeper, as it does during section B of the commute, Mrs. Washington is driving one mile per minute, or 60 miles per hour. As she drives through section C, she only drove 1 mile after 4 minutes, or 15 miles per hour.

4. She lives 20 miles from her office. This is stated in the question itself.