Answer:

Explanation:
According to the information of the problem
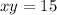
And
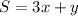
If you solve for
 on the first equation you get that
on the first equation you get that
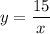
then you have that

If you find the derivative of the function you get that
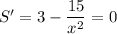
The equation has two possible solutions but you are looking for POSITIVE numbers that make
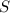 as small as possible.
as small as possible.
Then
