Question

The activation energy of an uncatalyzed reaction is 70 kJ/mol. When a catalyst is added, the activation energy (at 20 °C) is 42 kJ/mol. Theoretically, to what temperature (°C) would one have to heat the solution so that the rate of the uncatalyzed reaction is equal to the rate of the catalyzed reaction at 20 °C? Assume the frequency factor A is constant, and assume the initial concentrations are the same.

Answer 1

T = 215.33 °C

Step-by-step explanation:

The activation energy is given by the Arrhenius equation:

`k = Ae^{(-Ea)/(RT)}`

Where:

k: is the rate constant

A: is the frequency factor

Ea: is the activation energy

R: is the gas constant = 8.314 J/(K*mol)

T: is the temperature

We have for the uncatalyzed reaction:

Ea₁ = 70 kJ/mol

And for the catalyzed reaction:

Ea₂ = 42 kJ/mol

T₂ = 20 °C = 293 K

The frequency factor A is constant and the initial concentrations are the same.

Since the rate of the uncatalyzed reaction (k₁) is equal to the rate of the catalyzed reaction (k₂), we have:

`k_(1) = k_(2)`

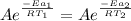`Ae^{(-Ea_(1))/(RT_(1))} = Ae^{(-Ea_(2))/(RT_(2))}` (1)

By solving equation (1) for T₁ we have:

`T_(1) = (T_(2)*Ea_(1))/(Ea_(2)) = (293 K*70 kJ/mol)/(42 kJ/mol) = 488. 33 K = 215.33 ^\circ C`

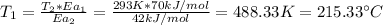
Therefore, we need to heat the solution at 215.33 °C so that the rate of the uncatalyzed reaction is equal to the rate of the catalyzed reaction.

I hope it helps you!