Answer:
The number of years after purchase at which Vishal's car will be worth $10,000 is
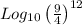 years
years
Explanation:
The relationship is given as follows
Value, V of the car = 22500×

Therefore, when the car is $10,000 we will have
$10,000 = 22,500×

Which will give;
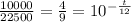
Hence;
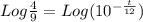
Therefore;
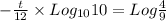
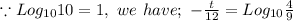
Which gives;
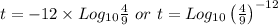
 years
years
Evaluated, the above equation becomes t = 4.226 years
Therefore, the number of years after purchase at which Vishal's car will be worth $10,000 =
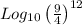 years.
years.