Answer:
The 95% confidence interval for p₁-p₂
( -0.01564 ,0.04044 )
Explanation:
Explanation:-
Given data Of the 1230 males surveyed, 176 responded that they had at least one tattoo
Given the first sample size 'n₁' = 1230
Given x = 176
The first sample proportion
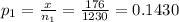
q₁ = 1-p₁ =1-0.1430 = 0.857
Given data Of the 1079 females surveyed, 141 responded that they had at least one tattoo
Given the second sample size n₂ = 1079
and x = 141
The second sample proportion
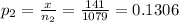
q₂ = 1-p₂ = 1-0.1306 =0.8694
The 95% confidence interval for p₁-p₂
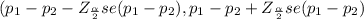
where
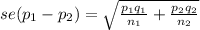
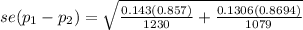
se(p₁-p₂) = 0.01431
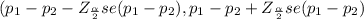
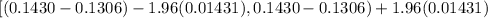
On calculation , we get
( 0.0124- 0.0280476 ,0.0124+ 0.0280476)
( -0.01564 ,0.04044 )
Conclusion:-
The 95% confidence interval to judge whether the proportion of males that have at least one tattoo differs significantly from the proportion of females that have at least one tattoo. Interpret the interval.
( -0.01564 ,0.04044 )