Question

A survey​ asked, "How many tattoos do you currently have on your​ body?" Of the 1230 males​ surveyed, 176 responded that they had at least one tattoo. Of the 1079 females​ surveyed, 141 responded that they had at least one tattoo. Construct a 95​% confidence interval to judge whether the proportion of males that have at least one tattoo differs significantly from the proportion of females that have at least one tattoo. Interpret the interval.

Answer 1

The 95​% confidence interval for p₁-p₂

( -0.01564 ,0.04044 )

Explanation:

Explanation:-

Given data Of the 1230 males​ surveyed, 176 responded that they had at least one tattoo

Given the first sample size 'n₁' = 1230

Given x = 176

The first sample proportion

`p_(1) = (x)/(n_(1) ) = (176)/(1230) =0.1430`

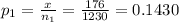
q₁ = 1-p₁ =1-0.1430 = 0.857

Given data Of the 1079 females​ surveyed, 141 responded that they had at least one tattoo

Given the second sample size n₂ = 1079

and x = 141

The second sample proportion

`p_(2) = (x)/(n_(2) ) = (141)/(1079) = 0.1306`

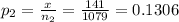
q₂ = 1-p₂ = 1-0.1306 =0.8694

The 95​% confidence interval for p₁-p₂

`(p_(1) - p_(2) - Z_{(\alpha )/(2) } se(p_(1) - p_(2)) ,p_(1) - p_(2) + Z_{(\alpha )/(2) } se(p_(1) - p_(2))`

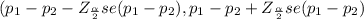
where

`se(p_(1)-p_(2)) = \sqrt{(p_(1)q_(1) )/(n_(1) )+(p_(2) q_(2) )/(n_(2) ) }`

`se(p_(1)-p_(2)) = \sqrt{(0.143(0.857) )/(1230)+( 0.1306(0.8694) )/(1079 )`

se(p₁-p₂) = 0.01431

`(p_(1) - p_(2) - Z_{(\alpha )/(2) } se(p_(1) - p_(2)) ,p_(1) - p_(2) + Z_{(\alpha )/(2) } se(p_(1) - p_(2))`

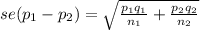
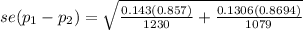
`[(0.1430-0.1306) - 1.96(0.01431) , 0.1430-0.1306) + 1.96(0.01431)`

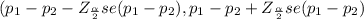
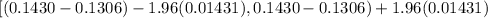
On calculation , we get

( 0.0124- 0.0280476 ,0.0124+ 0.0280476)

( -0.01564 ,0.04044 )

Conclusion:-

The 95​% confidence interval to judge whether the proportion of males that have at least one tattoo differs significantly from the proportion of females that have at least one tattoo. Interpret the interval.

( -0.01564 ,0.04044 )