Answer:
U = 5.37*10^33 J
Step-by-step explanation:
The gravitational potential energy between two bodies is given by:
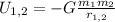
G: Cavendish's constant = 6.67*10^-11 m^3/kg.s
For three bodies the total gravitational potential energy is:
![U_(T)=U_(1,2)+U_(1,3)+U_(2,3)\\\\U_(T)=-G[(m_1m_2)/(r_(1,2))+(m_1m_3)/(r_(1,3))+(m_2m_3)/(r_(2,3))]](https://img.qammunity.org/2021/formulas/physics/college/el0bm2sdjr8zug33500be5zynmh5d4a98g.png)
BY replacing the values of the parameters for 1->earth, 2->moon and 3->sun you obtain:
![U_(T)=-(6.67*10^(-11)m^3/kg.s)[((5.98*10^(24)kg)(7.36*10^(22)kg))/(3.84*10^(8)m)+\\\\((5.98*10^(24)kg)(1.99*10^(30)kg))/(1.496*10^(11)m)+((7.36*10^(22)kg)(1.99*10^(30)kg))/(1.496*10^(11)m-3.84*10^8m)]\\\\U_(T)=5.37*10^(33)J](https://img.qammunity.org/2021/formulas/physics/college/z5kcp74uwvqwmrt5beca5vehs0a4aqvr3b.png)
hence, the total gravitational energy is 5.37*10^33 J