Question

During a solar eclipse, the Moon, Earth, and Sun all lie on the same line, with the Moon between the Earth and the Sun. The Moon has a mass of 7.36 × 1022 kg; the Earth has a mass of 5.98 × 1024 kg; and the Sun has a mass of 1.99 × 1030 kg. The distance between the Moon and the Earth is 3.84 × 108 m; the distance between the Earth and the Sun is 1.496 × 1011 m. Calculate the total gravitational potential energy for this arrangement.

Answer 1

U = 5.37*10^33 J

Step-by-step explanation:

The gravitational potential energy between two bodies is given by:

`U_(1,2)=-G(m_1m_2)/(r_(1,2))`

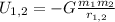
G: Cavendish's constant = 6.67*10^-11 m^3/kg.s

For three bodies the total gravitational potential energy is:

`U_(T)=U_(1,2)+U_(1,3)+U_(2,3)\\\\U_(T)=-G[(m_1m_2)/(r_(1,2))+(m_1m_3)/(r_(1,3))+(m_2m_3)/(r_(2,3))]`

BY replacing the values of the parameters for 1->earth, 2->moon and 3->sun you obtain:

`U_(T)=-(6.67*10^(-11)m^3/kg.s)[((5.98*10^(24)kg)(7.36*10^(22)kg))/(3.84*10^(8)m)+\\\\((5.98*10^(24)kg)(1.99*10^(30)kg))/(1.496*10^(11)m)+((7.36*10^(22)kg)(1.99*10^(30)kg))/(1.496*10^(11)m-3.84*10^8m)]\\\\U_(T)=5.37*10^(33)J`

hence, the total gravitational energy is 5.37*10^33 J