Given question is incomplete. The complete question is as follows.
When 72.8 g of benzamide (
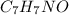 ) are dissolved in 600 g of a certain mystery liquid X, the freezing point of the solution is
) are dissolved in 600 g of a certain mystery liquid X, the freezing point of the solution is
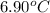 less than the freezing point of pure X. Calculate the mass of ammonium chloride
less than the freezing point of pure X. Calculate the mass of ammonium chloride
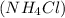 that must be dissolved in the same mass of X to produce the same depression in freezing point. The van't Hoff factor i = 70 for ammonium chloride in X. Be sure your answer has a unit symbol, if necessary, and round your answer to significant digits.
that must be dissolved in the same mass of X to produce the same depression in freezing point. The van't Hoff factor i = 70 for ammonium chloride in X. Be sure your answer has a unit symbol, if necessary, and round your answer to significant digits.
Step-by-step explanation:
The given data is as follows.
Mass of solute (benzamide),
 = 72.8 g
= 72.8 g
Mass of solvent (X),
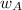 = 600 g
= 600 g
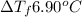
Molar mass of benzamide,
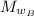 = 121.14 g/mol
= 121.14 g/mol
We know that,
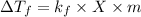 (for non-dissociating)
(for non-dissociating)
 ...... (1)
...... (1)
For other experiment, when
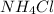 is taken :
is taken :
Mass of
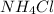 , (
, (
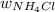 ) = ?
) = ?
Molar mass of
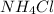 = 53.491 g/mol
= 53.491 g/mol
Mass of solvent (X) = 600 g

i = Van't Hoff factor = 1.70
As,
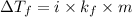
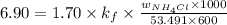 ........... (2)
........... (2)
Now, we will divide equation (1) by equation (2) as follows.
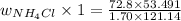
= 18.90 g
Therefore, we can conclude that the mass of ammonium chloride
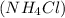 that must be dissolved in the same mass of X to produce the same depression in freezing point is 18.90 g.
that must be dissolved in the same mass of X to produce the same depression in freezing point is 18.90 g.