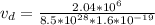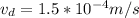Question

An eighteen gauge copper wire has a nominal diameter of 1.02mm. This wire carries a constant current of 1.67A to a 200w lamp. The density of free electrons is 8.5 x 1028 electrons per cubic metre. Find the magnitude of:

i. The current density ii. The drift velocity

Answer 1

The current density is
`J = 2.04 * 10^(6) A /m^2`

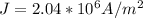
The drift velocity is
`v_d = 1.5 * 10^(-4) m/s`

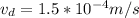
Step-by-step explanation:

From the question we are told that

The nominal diameter of the wire is
`d = 1.02 mm= (1.02)/(1000) = 0.00102 \ m`

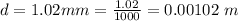
The current carried by the wire is
`I = 1.67 A`

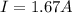
The power rating of the lamp is
`P = 200 W`

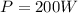
The density of electron is
`n = 8.5 * 10^(28) \ e/m^3`

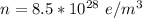
The current density is mathematically represented as

`J = (I)/(A)`

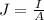
Where A is the area which is mathematically evaluated as

`A = \pi (d^2)/(4)`

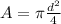
Substituting values

`A = 3.142 * ((1.02 * 10^(-3))^2 )/(4)`

`A = 8.0*10^(-4)m^2`

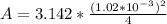
So

`J = (1.67)/(8.0*10^(-4))`

`J = 2.04 * 10^(6) A /m^2`

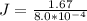
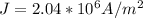
The drift velocity is mathematically represented as

`v_d = (J)/(ne)`

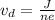
Where e is the charge on one electron which has a value
`e = 1.602 *10^(-19) C`

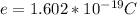
So

`v_d =(2.04 * 10^6 )/(8.5 *10^(28) * 1.6 * 10^(-19))`

`v_d = 1.5 * 10^(-4) m/s`