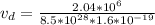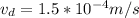Answer:
The current density is

The drift velocity is
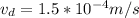
Step-by-step explanation:
From the question we are told that
The nominal diameter of the wire is

The current carried by the wire is
The power rating of the lamp is
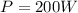
The density of electron is

The current density is mathematically represented as

Where A is the area which is mathematically evaluated as
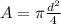
Substituting values
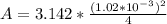

So


The drift velocity is mathematically represented as

Where e is the charge on one electron which has a value
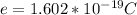
So