Question

A cylindrical bar of metal having a diameter of 21.0 mm and a length of 210 mm is deformed elastically in tension with a force of 46800 N. Given that the elastic modulus and Poisson's ratio of the metal are 60.9 GPa and 0.34, respectively, determine the following: (a) The amount by which this specimen will elongate in the direction of the applied stress. (b) The change in diameter of the specimen. Indicate an increase in diameter with a positive number and a decrease with a negative number. (a) 0.443 mm (b) mm

Answer 1

The the elongated length is
`\Delta L = 0.4 \ mm`

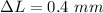
The change in diameter is
`\Delta d = - 0.0136\ mm`

Step-by-step explanation:

From the question we are told that

The diameter of the cylindrical bar is
`d = 21.0 \ mm = (21)/(1000) = 0.021 \ m`

The length of the cylindrical bar is
`L= 210 \ mm = 0.21 \ m`

The force that deformed it is
`F = 46800 \ N`

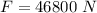
Elastic modulus is
`E = 60.9 \ GPa = 60.9 *10^(9)Pa`

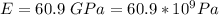
The Poisson's ratio is
`\mu = 0.34`

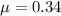
Generally elastic modulus is mathematically represented as

`E = (\sigma )/(\epsilon)`

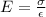
Where

`\epsilon` is the strain which is mathematically represented as

`\epsilon = (L)/(\Delta L)`

Where
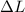`\Delta L` is the elongation length

`\sigma` is the stress on the cylinder which is mathematically represented as

`\sigma = (F)/(A)`

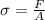
Where F is the force and

A is the area which is calculated as

`A = \frac{\pi} {4} d^2`

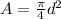
Substituting values

`A = (\pi)/(4) * (0.021)`

`A = 0.000346 \ m^2`

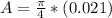
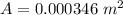
So the stress is

`\sigma = (46800)/(0.000346)`

`\sigma = 1.35 *10^(8) \ N \cdot m^2`

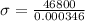
Thus the elastic modulus is

`E = (1.35 *10 ^(8))/((\Delta L)/(L) )`

making
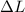`\Delta L` the subject

`\Delta L = (EL)/(1.35 *10^(8))`

Substituting values

`\Delta L = (1.35 *10^(8) * 0.21)/(1.35 *10^(8))`

`\Delta L = (1.35 *10^(8) * 0.21)/(60.9*10^(9))`

`\Delta L = 0.0004 \ m`

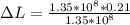
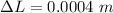
Converting to mm

`\Delta L = 0.0004 * 1000`

`\Delta L = 0.4 \ mm`

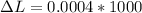
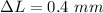
Generally the poisson ratio is mathematically represented as

`\mu = - ((\Delta d )/(d) )/((\Delta L )/(L) )`

The negative sign indicate a decrease in diameter as a result of the force

making
`\Delta d` the subject

`\Delta d = - \mu * (\Delta L )/(L ) * d`

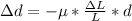
Substituting values

`\Delta d = - 0.34 * (0.0004 )/(0.210 ) * 0.021`

`\Delta d = - 1.36 *10^(-5) \ m`

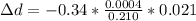
Converting to mm

`\Delta d = - 0.0136\ mm`