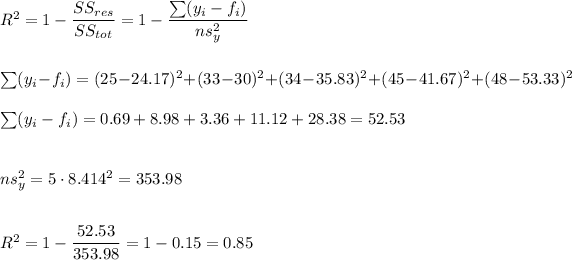Answer:
1) b1=5.831
2) b0=12.510
3) y(34)=210.764
4) y(0)=12.510
5) y=12.510+5.831x
6) R^2=0.85
Explanation:
We have the linear regression model
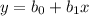 .
.
We start by calculating the all the parameters needed to define the model:
- Mean of x:
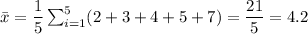
- Uncorrected standard deviation of x:
![s_x=\sqrt{(1)/(n)\sum_(i=1)^(5)(x_i-\bar x)^2}\\\\\\s_x=\sqrt{(1)/(5)\cdot [(2-4.2)^2+(3-4.2)^2+(4-4.2)^2+(5-4.2)^2+(7-4.2)^2]}\\\\\\ s_x=\sqrt{(1)/(5)\cdot [(4.84)+(1.44)+(0.04)+(0.64)+(7.84)]}\\\\\\ s_x=\sqrt{(14.8)/(5)}=√(2.96)\\\\\\s_x=1.72](https://img.qammunity.org/2021/formulas/mathematics/college/jnp5ltle8lnvij9c6teuzfz2zvsso4et8c.png)
- Mean of y:
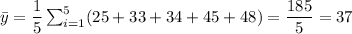
- Standard deviation of y:
![s_y=\sqrt{(1)/(n)\sum_(i=1)^(5)(y_i-\bar y)^2}\\\\\\s_y=\sqrt{(1)/(5)\cdot [(25-37)^2+(33-37)^2+(34-37)^2+(45-37)^2+(48-37)^2]}\\\\\\ s_y=\sqrt{(1)/(5)\cdot [(144)+(16)+(9)+(64)+(121)]}\\\\\\ s_y=\sqrt{(354)/(5)}=√(70.8)\\\\\\s_y=8.414](https://img.qammunity.org/2021/formulas/mathematics/college/vooqb5eyeeeoxb2mazk14jh9zpssp1yk23.png)
- Sample correlation coefficient
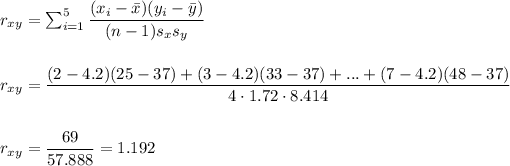
Step 1
The slope b1 can be calculated as:
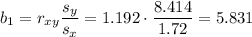
Step 2
The y-intercept b0 can now be calculated as:
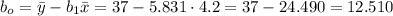
Step 3
The estimated value of y when x=34 is:
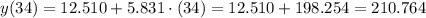
Step 4
At x=0, the estimated y takes the value of the y-intercept, by definition.
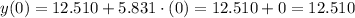
Step 5
The linear model becomes
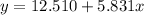
Step 6
The coefficient of determination can be calculated as: