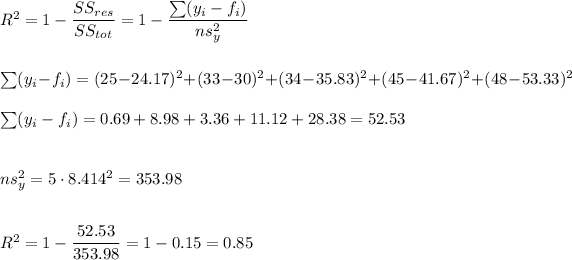Question

The table below gives the list price and the number of bids received for five randomly selected items sold through online auctions. Using this data, consider the equation of the regression line, yˆ=b0+b1x, for predicting the number of bids an item will receive based on the list price. Keep in mind, the correlation coefficient may or may not be statistically significant for the data given. Remember, in practice, it would not be appropriate to use the regression line to make a prediction if the correlation coefficient is not statistically significant.

Price in Dollars 25 33 34 45 48
Number of Bids 2 3 4 5 7

Step 1 of 6: Find the estimated slope. Round your answer to three decimal places.
Step 2 of 6: Find the estimated y-intercept. Round your answer to three decimal places.Step 3 of 6: Find the estimated value of y when x = 34. Round your answer to three decimal places.Step 4 of 6: Determine the value of the dependent variable yˆ at x = 0.Step 5 of 6: Substitute the values you found in steps 1 and 2 into the equation for the regression line to find the estimated linear model. According to this model, if the value of the independent variable is increased by one unit, then find the change in the dependent variable yˆ.Step 6 of 6: Find the value of the coefficient of determination.

Answer 1

1) b1=5.831

2) b0=12.510

3) y(34)=210.764

4) y(0)=12.510

5) y=12.510+5.831x

6) R^2=0.85

Explanation:

We have the linear regression model
`y=b_0+b_1 x`.

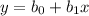We start by calculating the all the parameters needed to define the model:

- Mean of x:

`\bar x=(1)/(5)\sum_(i=1)^(5)(2+3+4+5+7)=(21)/(5)=4.2`

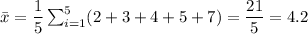
- Uncorrected standard deviation of x:

`s_x=\sqrt{(1)/(n)\sum_(i=1)^(5)(x_i-\bar x)^2}\\\\\\s_x=\sqrt{(1)/(5)\cdot [(2-4.2)^2+(3-4.2)^2+(4-4.2)^2+(5-4.2)^2+(7-4.2)^2]}\\\\\\ s_x=\sqrt{(1)/(5)\cdot [(4.84)+(1.44)+(0.04)+(0.64)+(7.84)]}\\\\\\ s_x=\sqrt{(14.8)/(5)}=√(2.96)\\\\\\s_x=1.72`

- Mean of y:

`\bar y=(1)/(5)\sum_(i=1)^(5)(25+33+34+45+48)=(185)/(5)=37`

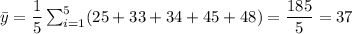
- Standard deviation of y:

`s_y=\sqrt{(1)/(n)\sum_(i=1)^(5)(y_i-\bar y)^2}\\\\\\s_y=\sqrt{(1)/(5)\cdot [(25-37)^2+(33-37)^2+(34-37)^2+(45-37)^2+(48-37)^2]}\\\\\\ s_y=\sqrt{(1)/(5)\cdot [(144)+(16)+(9)+(64)+(121)]}\\\\\\ s_y=\sqrt{(354)/(5)}=√(70.8)\\\\\\s_y=8.414`

- Sample correlation coefficient

`r_(xy)=\sum_(i=1)^5((x_i-\bar x)(y_i-\bar y))/((n-1)s_xs_y)\\\\\\r_(xy)=((2-4.2)(25-37)+(3-4.2)(33-37)+...+(7-4.2)(48-37))/(4\cdot 1.72\cdot 8.414)\\\\\\r_(xy)=(69)/(57.888)=1.192`

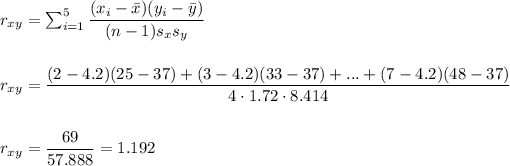
Step 1

The slope b1 can be calculated as:

`b_1=r_(xy)(s_y)/(s_x)=1.192\cdot(8.414)/(1.72)=5.831`

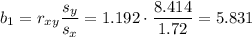
Step 2

The y-intercept b0 can now be calculated as:

`b_o=\bar y-b_1\bar x=37-5.831\cdot 4.2=37-24.490=12.510`

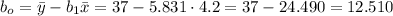
Step 3

The estimated value of y when x=34 is:

`y(34)=12.510+5.831\cdot(34)=12.510+198.254=210.764`

Step 4

At x=0, the estimated y takes the value of the y-intercept, by definition.

`y(0)=12.510+5.831\cdot(0)=12.510+0=12.510`

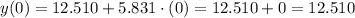
Step 5

The linear model becomes

`y=12.510+5.831x`

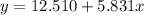
Step 6

The coefficient of determination can be calculated as:

`R^2=1-(SS_(res))/(SS_(tot))=1-(\sum(y_i-f_i))/(ns_y^2)\\\\\\\sum(y_i-f_i)=(25-24.17)^2+(33-30)^2+(34-35.83)^2+(45-41.67)^2+(48-53.33)^2\\\\\sum(y_i-f_i)=0.69+ 8.98+ 3.36+ 11.12+ 28.38=52.53\\\\\\ ns_y^2=5\cdot 8.414^2=353.98\\\\\\R^2=1-(52.53)/(353.98)=1-0.15=0.85`