Question

After getting trounced by your little brother in a​ children's game, you suspect the die he gave you to roll may be unfair. To​ check, you roll it 60 ​times, recording the number of times each face appears. Do these results cast doubt on the​ die's fairness? Full data set Face Count Face Count 1 14 4 15 2 5 5 14 3 11 6 1 ​a) If the die is​ fair, how many times would you expect each face to​ show? nothing ​b) To see if these results are​ unusual, will you test​ goodness-of-fit, homogeneity, or​ independence? A. Independence B. Homogeneity C. ​Goodness-of-fit ​c) State your hypotheses. A. Upper H 0​: The die is unfair. Upper H Subscript Upper A​: The die is fair. B. Upper H 0​: The die is fair. Upper H Subscript Upper A​: The die produces outcomes that are less than the expected value. C. Upper H 0​: The die is fair. Upper H Subscript Upper A​: The die is unfair. D. Upper H 0​: The die is fair. Upper H Subscript Upper A​: The die produces outcomes that are greater than the expected value. ​d) Check the conditions. Is the counted data condition​ met? No Yes Is the randomization condition​ met? Yes No Is the expected cell frequency condition​ met? Yes No ​e) How many degrees of freedom are​ there? nothing

Answer 1

Given:

Face ____________Count

1_________________14

4_________________15

2_________________5

5_________________14

3_________________11

6_________________1

a) I rolled the die 60 times and my values are recorded.

Assuming the die is fair, each face is expected to show 10 times.

`60* (1)/(6) = 10`

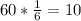
b) To check if my results are unusual hypothesis test is used to address this. In this case the test is called goodness of fit.

c) For the null and alternative hypothesis :

The null hypothesis states , the die is fair (the number of times each face appear is equal)

The alternative hypothesis states the die is not fair.

H0 : p = 0.6

H1 : p ≠ 0.6

d)

The number of times the die is rolled is recorded.

The number of times the die is rolled is independent because the outcomes are independent.

Here the expected value of observation is more than five because the null hypothesis expects each die roll to be 10. Thus, the condition is satisfied.

e) Number of degrees of freedom for this test is n-1.

n = 6 (total faces in a die)

Therefore, degrees of freedom =

6-1 = 5