Question

A particle of positive charge ???? is assumed to have a fixed position at P. A second particle of mass m and negative charge −q moves at constant speed in a circle of radius r1, centered at P. Derive an expression for the work W that must be done by an external agent in the second particle in order to increase the radius of the circle of motion, centered at P, to r2.

Answer 1

`W=(1)/(2)kq_1q_2[(1)/(r_2)-(1)/(r_1)]`

Step-by-step explanation:

To find the work W to put the negative charge in the new orbit you can use the following formula:

`W=\Delta K\\\\K=(1)/(2)mv^2`

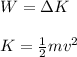
That is, the total work is equal to the change in the kinetic energy of the negative charge. Then you calculate the speed of the electron, by using the second Newton Law and the expression for the electrostatic energy:

`F=ma_c\\\\-k((q_1)(q_2))/(r_1^2)=m(v^2)/(r_1)\\\\v^2=k(q_1q_2)/(mr_1)`

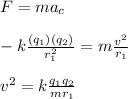
r1: radius of the first orbit

m: mass of the negative charge

v: velocity of the charge

k: Coulomb's constant

q1: charge of the fixed particle at point P

q2: charge of the negative charge

Hence, the velocity of the charge in a new orbit with radius r2 is:

`v'^2=k(q_1q_2)/(mr_2)`

Finally the work required to put the charge in the new orbit is:

`W=\Delta K =(1)/(2)m[v'^2-v^2]\\\\W=(1)/(2)m[k(q_1q_2)/(mr_2)-k(q_1q_2)/(mr_1)]\\\\W=(1)/(2)kq_1q_2[(1)/(r_2)-(1)/(r_1)]`