Question

A random sample of 8989 eighth grade​ students' scores on a national mathematics assessment test has a mean score of 282282. This test result prompts a state school administrator to declare that the mean score for the​ state's eighth graders on this exam is more than 280280. Assume that the population standard deviation is 3838. At alphaαequals=0.050.05​, is there enough evidence to support the​ administrator's claim? Complete parts​ (a) through​ (e).

Answer 1

To determine if there is enough evidence to support the administrator's claim, we need to perform a hypothesis test. By comparing the z-score to the critical value at α=0.05, we can reject the null hypothesis and conclude that there is enough evidence to support the administrator's claim.

Step-by-step explanation:

To determine if there is enough evidence to support the administrator's claim, we need to perform a hypothesis test. The null hypothesis (H0) is that the mean score for the state's eighth graders is <=280. The alternative hypothesis (Ha) is that the mean score is >280.

To conduct the test, we can calculate the z-score using the formula z = (x - μ) / (σ / sqrt(n)), where x is the sample mean, μ is the hypothesized population mean (280), σ is the population standard deviation (38), and n is the sample size (8989). Plug in the given values, we get z = (282 - 280) / (38 / sqrt(8989)) = 3.055.

Next, we compare the z-score to the critical value at α=0.05. For a one-tailed test, the critical value is 1.645. Since 3.055 > 1.645, we reject the null hypothesis and conclude that there is enough evidence to support the administrator's claim that the mean score for the state's eighth graders on this exam is more than 280.

Answer 2

`t=(282-280)/((38)/(√(89)))=0.497`

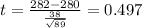
Now we can calculate the p value for the test

We are conducting a right tailed test so then the p value is given by:

`p_v =P(z>0.497)=0.310`

Since the p value is higher than the significance level we have enough evidence to conclude that the true mean is not significantly higher than 280 so then the administrator claim is not true

Step-by-step explanation:

Data provided

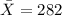`\bar X=282` represent the mean for the assesment test

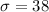`\sigma=38` represent the population deviation

`n=89` sample size

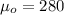`\mu_o =280` represent the value to verify

`\alpha=0.05` represent the significance level

t would represent the statistic

`p_v` represent the p value

Hypothesis to test

We want to determine if the mean score for the​ state's eighth graders on this exam is more than 280, so then the system of hypothesis would be:

Null hypothesis:
`\mu \leq 280`

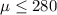
Alternative hypothesis:
`\mu > 280`

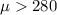
Since we know the population deviation we can use a z test for the true mean and the statistic is given by:

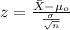`z=(\bar X-\mu_o)/((\sigma)/(√(n)))` (1)

Replacing the info given by the problem we got:

`t=(282-280)/((38)/(√(89)))=0.497`

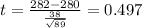
Now we can calculate the p value for the test

We are conducting a right tailed test so then the p value is given by:

`p_v =P(z>0.497)=0.310`

Since the p value is higher than the significance level we have enough evidence to conclude that the true mean is not significantly higher than 280 so then the administrator claim is not true