Question

Lisa, a dentist, believes not enough teenagers floss daily. She would like to test the claim that the proportion of teenagers who floss twice a day is less than 40%. To test this claim, a group of 400 teenagers are randomly selected and its determined that 149 floss twice a day.

Answer 1

`z=\frac{0.3725 -0.4}{\sqrt{(0.4(1-0.4))/(400)}}=-1.123`

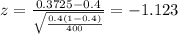
The p value for a left tailed test would be:

`p_v =P(z<-1.123)=0.131`

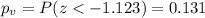
Since the p value is very higher we can conclude that the true proportion of teenagers who floss twice a day is NOT less than 40%.

Explanation:

Information given

n=400 represent the random sample given

X=149 represent the floss twice a day

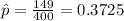`\hat p=(149)/(400)=0.3725` estimated proportion of floss twice a day

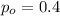`p_o=0.4` is the value the proportion that we want to check

z would represent the statistic

`p_v` represent the p value

System of hypothesis

We want to check proportion of teenagers who floss twice a day is less than 40%, so then the system of hypothesis are.:

Null hypothesis:
`p \geq 0.4`

Alternative hypothesis:
`p < 0.4`

For the one sample proportion test the statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

If we replace the info given we got:

`z=\frac{0.3725 -0.4}{\sqrt{(0.4(1-0.4))/(400)}}=-1.123`

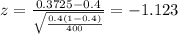
The p value for a left tailed test would be:

`p_v =P(z<-1.123)=0.131`

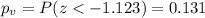
Since the p value is very higher we can conclude that the true proportion of teenagers who floss twice a day is NOT less than 40%.