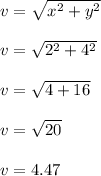Question

What function do you use to find the angle of a vector, when you know its components?

Answer 1

`\theta = tan^(-1)((y)/(x))`

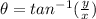
Explanation:

If we are given components of a vector then we can find the angle between them.

Suppose we are given a vector v

`v = (x, y)`

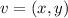
Where x is the horizontal component and y is the vertical component.

The angle can be found by using

`tan(\theta)=(y)/(x)\\\\\theta = tan^(-1)((y)/(x))`

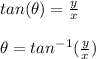
The magnitude of the vector v can be found using

`v = \sqrt{x^(2)+y^(2)}`

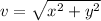
Example:

Lets do a quick example:

`v = (2, 4)`

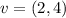
The angle of the vector is

`tan(\theta)=(4)/(2)\\\\\theta = tan^(-1)((4)/(2))\\\\\theta = 63.43^(\circ)`

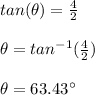
The magnitude of the vector is

`v = \sqrt{x^(2)+y^(2)}\\\\v = \sqrt{2^(2)+4^(2)}\\\\v = √(4+16)\\\\v = √(20)\\\\v = 4.47`