Question

What’s the distance between point A (32,15) and point B (32,29

Answer 1

`d = √((32-32)^2 +(15-29)^2) = √(196)= 14`

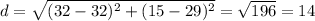
So then we can conclude that the smallest distance between the point A (32,15) and the point B(32,39) is 14

Explanation:

When we have a two points on a dimensional space A and B we can find the distance between the two points with the following formula:

`d= √((x_A -x_B)^2 +(y_A -y_B)^2)`

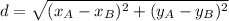
Where (x_A,y_A) represent the coordinates for the point A and (x_B,y_B) represent the coordinates for the point B. And we know that the coordinates are :

A= (32,15) and B= (32,29)

And replacing in the formula for the distance we got:

`d = √((32-32)^2 +(15-29)^2) = √(196)= 14`

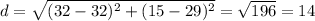
So then we can conclude that the smallest distance between the point A (32,15) and the point B(32,39) is 14

Answer 2

14 units

Explanation:

Both points lie on the vertical line x=32, so the distance between them is the difference of their y-coordinates:

29 -15 = 14 . . . . units

The two points are 14 units apart.