Question

Q 3.19: In 2011 and 2015, the study was held to determine the proportion of people who read books. 948 people of 1200 said they read at least one book in the last 3 months in 2011. 1080 people of 1500 said they read at least one book in the last 3 months in 2015. Find the 95% confidence interval for the difference in proportions.

Answer 1

`(0.79-0.72) -1.96 \sqrt{(0.79(1-0.79))/(1200) +(0.72(1-0.72))/(1500)} =0.0376`

`(0.79-0.72) +1.96 \sqrt{(0.79(1-0.79))/(1200) +(0.72(1-0.72))/(1500)} =0.1024`

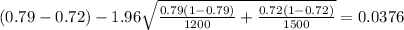
And the 95% confidence interval for the difference of the two proportions is given by:

`0.0376 \leq p_1 -p_2 \leq 0.1024`

Explanation:

For this case we have the following info given:

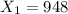`X_1 = 948` number of people that they read at least one book in the last 3 months in 2011

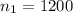`n_1 = 1200` the sample size selected for 2011

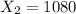`X_2 = 1080` number of people that they read at least one book in the last 3 months in 2015

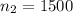`n_2 = 1500` the sample size selected for 2015

The estimated proportions people that they read at least one book in the last 3 months for each year are given by:

`\hat p_1 = (948)/(1200)= 0.79`

`\hat p_2 = (1080)/(1500)= 0.72`

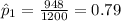
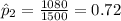
And the confidence interval for the true difference of proportions is given by:

`(\hat p_1 -\hat p_2) \pm z_(\alpha/2) \sqrt{(\hat p_1 (1-\hat p_1))/(n_1) +(\hat p_2 (1-\hat p_2))/(n_2)}`

The confidence level is 95% so then the significance is 0.05 or 5% and
`\alpha/2 =0.025` and the critical value for this case using the normal standard distribution is:

`z_(\alpha/2)=\pm 1.96`

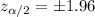
And replacing into the confidence interval formula we got:

`(0.79-0.72) -1.96 \sqrt{(0.79(1-0.79))/(1200) +(0.72(1-0.72))/(1500)} =0.0376`

`(0.79-0.72) +1.96 \sqrt{(0.79(1-0.79))/(1200) +(0.72(1-0.72))/(1500)} =0.1024`

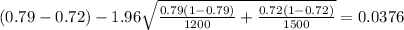
And the 95% confidence interval for the difference of the two proportions is given by:

`0.0376 \leq p_1 -p_2 \leq 0.1024`