Answer:
We want to find the percentage of values between 147700 and 152300
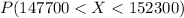
And one way to solve this is use a formula called z score in order to find the number of deviations from the mean for the limits given:
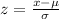
And replacing we got:
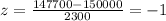
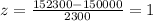
So then we are within 1 deviation from the mean so then we can conclude that the percentage of values between $147,700 and $152,300 is 68%
Explanation:
We define the random variable representing the prices of a certain model as X and the distirbution for this random variable is given by:

The empirical rule states that within one deviation from the mean we have 68% of the data, within 2 deviations from the mean we have 95% and within 3 deviations 99.7 % of the data.
We want to find the percentage of values between 147700 and 152300
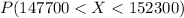
And one way to solve this is use a formula called z score in order to find the number of deviations from the mean for the limits given:
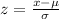
And replacing we got:
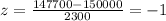
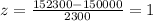
So then we are within 1 deviation from the mean so then we can conclude that the percentage of values between $147,700 and $152,300 is 68%