Question

Suppose that a parallel-plate capacitor has circular plates with radius R = 26 mm and a plate separation of 4.0 mm. Suppose also that a sinusoidal potential difference with a maximum value of 220 V and a frequency of 76 Hz is applied across the plates; that is, V = (220 V) sin[2π(76 Hz)t]. Find Bmax(R), the maximum value of the induced magnetic field that occurs at r = R.

Answer 1

B(max) = 3.7971 ×
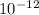`10^(-12)` T

Step-by-step explanation:

given data

radius R = 26 mm

plate separation d = 4.0 mm

potential difference Vm = 220 V

frequency f = 76 Hz

V = (220 V) sin[2π(76 Hz)t]

solution

we know that E will be

E = V ÷ d ............1

put here value

E =
`(220 * sin(2\pi 76* t))/(d)`

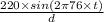
and here we take as given r = R

so A = π R² .................2

and

ФE = E × A

ФE =
`(\pi R^2 * 220 * sin(2\pi 76 * t))/(d)` .....................3

so use use here now Ampere's Law that is

∫ B ds =
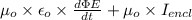`\mu_o * \epsilon_o * (d\Phi E)/(dt) + \mu_o * I_(encl)` .....................4

and

here
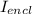`I_(encl)` is = 0 and r = R

so

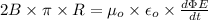`2B * \pi * R = \mu_o * \epsilon_o * (d\Phi E)/(dt)` .....................5

and put here value we get

B =
`(\mu_o * \epsilon_o * \pi * f * R * V_m cos(2\pi f t))/(d)` .....................6

put here value for B maximum cos(2πft) = 1

and we get B (max)

B(max) =
`(\mu_o* \epsilon_o* \pi * f* R* V_m)/(d)` ....................7

put here all value

B(max) =
`(4\pi *10^(-7) * 8.85* 10^(-12)* \pi * 76 * 0.026* 220 )/(4* 10^(-3))`

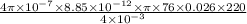
solve it we get

B(max) = 3.7971 ×
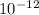`10^(-12)` T