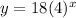Question

Write an exponential function in the form y = ab that goes through points (0,18)

and (2,288).

Answer 1

`18 = ab^0 =a`

And using the second point we have this:

`288= 18 b^2`

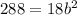
If we divide both sides by 18 we got:

`16 = b^2`

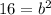
And taking the square roof of 16 we got:

`b =\pm √(16) =\pm 4`

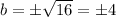
But on this case the negative solution not makes sense since the function is increasing so then the correct exponential function that pass through the points (0,18) and (2,288) is:

`y = 18 (4)^x`

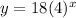
Explanation:

We want to construct an exponential function given by this general form:

`y = ab^x`

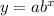
And we know that the function needs to pass for two points (0,18) and (2,288). Using the first point we have this:

`18 = ab^0 =a`

And using the second point we have this:

`288= 18 b^2`

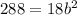
If we divide both sides by 18 we got:

`16 = b^2`

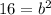
And taking the square roof of 16 we got:

`b =\pm √(16) =\pm 4`

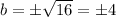
But on this case the negative solution not makes sense since the function is increasing so then the correct exponential function that pass through the points (0,18) and (2,288) is:

`y = 18 (4)^x`