Question

In ΔBCD, the measure of ∠D=90°, the measure of ∠C=42°, and CD = 7.5 feet. Find the length of DB to the nearest tenth of a foot.

Answer 1

We have been given that in ΔBCD, the measure of ∠D=90°, the measure of ∠C=42°, and CD = 7.5 feet. We are asked to find the length of DB to nearest tenth of foot.

First of all, we will draw a right triangle using our given information.

We can see from the attachment that DB is opposite side to angle C and CD is adjacent side to angle.

We know that tangent relates opposite side of right triangle to adjacent side of right triangle.

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

`\text{tan}(\angle C)=(DB)/(CD)`

`\text{tan}(42^(\circ))=(DB)/(7.5)`

`7.5\cdot\text{tan}(42^(\circ))=(DB)/(7.5)\cdot 7.5`

`7.5\cdot\text{tan}(42^(\circ))=DB`

`7.5\cdot0.900404044298=DB`

`DB=7.5\cdot0.900404044298`

`DB=6.753030332235\approx 6.8`

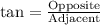
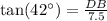
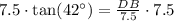
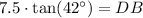
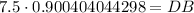
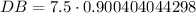
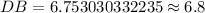
Therefore, the length of DB is approximately 6.8 feet.