Answer:
B) increase by 0.18 V
Step-by-step explanation:
The given chemical spontaneous reaction is :

By applying Nernst Equation:
![E_(cell) = E^0 - (0.059)/(n) log [(product)/(reactant)]](https://img.qammunity.org/2021/formulas/chemistry/college/tywxnmdqxfb5r80vu9o1ywjw1g7z4339n0.png)
here ;
n = number of electrons transferred in the reaction
n =2
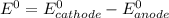
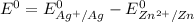

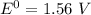
When it happens to occur that the concentration of chlorine (aq) and Zn²⁺ (aq) is 1 M ;
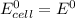 is as follows:
is as follows:
![E_(cell) = E^0 - (0.059)/(n) log [(product)/(reactant)]](https://img.qammunity.org/2021/formulas/chemistry/college/tywxnmdqxfb5r80vu9o1ywjw1g7z4339n0.png)
![E_(cell) = 1.56 - (0.059)/(n) log [([Zn^(2+)])/([Cl^-]^2)]](https://img.qammunity.org/2021/formulas/chemistry/college/mc0f8yv5lk4hij0t88zmg46kg22n7dzcpv.png)
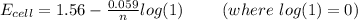

Now; the
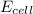 value in the decreased concentration of chlorine (aq) ion is calculated as:
value in the decreased concentration of chlorine (aq) ion is calculated as:
![E_(cell) = E^0 - (0.059)/(n) log [(product)/(reactant)]](https://img.qammunity.org/2021/formulas/chemistry/college/tywxnmdqxfb5r80vu9o1ywjw1g7z4339n0.png)
![E_(cell) = 1.56 - (0.059)/(n) log [([Zn^(2+)])/([Cl^-]^2)]](https://img.qammunity.org/2021/formulas/chemistry/college/mc0f8yv5lk4hij0t88zmg46kg22n7dzcpv.png)
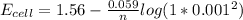
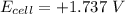
Hence; the change in voltage =
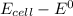
= 1.737 - 1.56
= 0.177 V
≅ 0.18 V
We therefore conclude that: since the
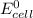 value after the decreased concentration of Chlorine is greater than the
value after the decreased concentration of Chlorine is greater than the
 before the change; then there is increase in the value by 0.18 V
before the change; then there is increase in the value by 0.18 V