Question

since 2010 the town of fall river has been experiencing a growth in population according to the model what will the population of fall river be in 2020

Answer 1

By 2020 the population of Fall River will be 48558

Explanation:

Here, we note that the equation for the model is p(t) = 36,800×2^(t/25)

That is the format;

`p(t) = 36,800 * 2^{(t)/(25)`

Where:

t = Number of years since 2010

Therefore, the population of the town in 2020 can be found by first finding the number of years between 220 and 2010 and plugging the value into the equation as follows;

Number of years, t = 2020 - 2010 = 10 years

Hence;

`p(t) = 36,800 * 2^{(10)/(25)} = 48557.89 \approx 48558`

Therefore, according to the model, by 2020 the population of Fall River will be 48558.

Answer 2

the population of fall river will be 48558

Explanation:

I think your question is missed of key information, allow me to add in and hope it will fit the original one.

Since 2010, the town of Fall River has been experiencing a growth in population. The relationship between the elapsed time, t, in years, since 2010 and the town's population, P(t left parenthesis, t, right parenthesis, is modeled by the following function. P(t)=36,800⋅
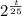`2^{(t)/(25) }` According to the model, what will the population of Fall River be in 2020? Round your answer, if necessary, to the nearest whole number.

My answer:

Given the exponential function:

P(t)=36,800⋅
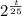`2^{(t)/(25) }` where:

• t in years, since 2010
• the town's population, P(t)

As we know, from 2010 to 2010 are 10 years

Hence, to find the population of fall river be in 2020, we substitute t =10 into the given function:

`P(10)=36800\cdot2^{^(10)/(25)}}\\=48557.9\\\approx 48558`

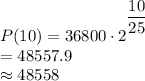
So in 2020, the population of fall river will be 48558

Hope it will find you well.