Question

Determine how fast the length of an edge of a cube is changing at the moment when the length of the edge is 5cm and the volume of the edge is decreasing at the rate of 100cm^3/sec​

Answer 1

1.333 cm/s

Step-by-step explanation:

The formula for the volume of the cube V in term of its edge s is:

`V = s^3`

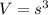
By using chain rule we have the following equation between the rate of change of the volume and the rate of change of the edge:

`(dV)/(dt) = (dV)/(ds)(ds)/(dt)`

`100 = (d(s^3))/(ds)(ds)/(dt)`

`100 = 3s^2(ds)/(dt)`

`(ds)/(dt) = (100)/(3s^2)`

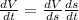
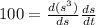
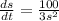
We can substitute s = 5 cm:

`(ds)/(dt) = (100)/(3*5^2) = 100 / 75 = 1.333 cm/s`