Answer:
9.0 ft (nearest tenth)
Explanation:
The chord is the base of an isosceles triangle with sides of the radius.
To calculate the approximate distance of the chord from the center of the circle, we need to find the height of this triangle.
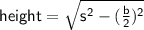
(where s is the side length and b is the base length of an isosceles triangle)
Given:
- s = radius = 10.8 ft
- b = chord = 12 ft
