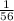Answer:
The exact probability that all three marbles drawn will be red is
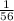
Explanation:
Number of red marbles = 5
Number of blue marbles = 4
Number of Green marbles = 7
Total Number of marbles = 5+4+7=16
We are given that three marbles are drawn out of the bag
Probability of getting 1 red marble on first draw=
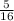
Probability of getting 1 red marble on second draw=
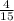
Probability of getting 1 red marble on third draw=
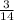
So,the exact probability that all three marbles drawn will be red=

Hence The exact probability that all three marbles drawn will be red is