Answer:
The probability is 1/8.
Explanation:
Two find the final probability asked, first we need to find each probability.
Probability of a card with S or E.
This probability is defined by the sum of the probability of getting a card with S, and a probability of getting a card with E. Remeber, when the probability involves "or", that means sum.
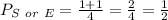
Probability of a tile with 2.
There are two tiles only, and one of them is numbered 2. So, its probability is
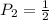
Probability of a red disc.
There are two discs only. So, the probability of getting a red disc is
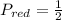
Now, the combined probabilty of all these events can be found by multiplying, because we want to now the chances of getting all these results which are independent.

Therefore, the probability is 1/8.