Question

In a game, four cards are labeled N, S, E, and W. Two tiles are numbered 1 and 2. Two discs are red and blue. A player randomly selects one card, one tile, and one disc.

Find the probability the player selects a card with S or E, a tile with 2, and a red disc.

Answer 1

The probability is 1/8.

Explanation:

Two find the final probability asked, first we need to find each probability.

Probability of a card with S or E.

This probability is defined by the sum of the probability of getting a card with S, and a probability of getting a card with E. Remeber, when the probability involves "or", that means sum.

`P_(S \ or \ E) =(1+1)/(4)=(2)/(4) =(1)/(2)`

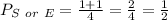
Probability of a tile with 2.

There are two tiles only, and one of them is numbered 2. So, its probability is

`P_(2)=(1)/(2)`

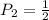
Probability of a red disc.

There are two discs only. So, the probability of getting a red disc is

`P_(red)=(1)/(2)`

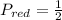
Now, the combined probabilty of all these events can be found by multiplying, because we want to now the chances of getting all these results which are independent.

`P_(total)=(1)/(2) * (1)/(2) * (1)/(2) =(1)/(8)`

Therefore, the probability is 1/8.