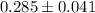Question

Express the confidence interval

24.4

%

<

p

<

32.6

%

in the form of

ˆ

p

±

M

E

.

Answer 1

`\hat p = (0.244+0.326)/(2)=0.285`

`ME = (0.326-0.244)/(2)=0.041`

`0.285 \pm 0.041`

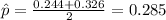
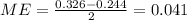
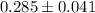
Explanation:

For this case we have a confidence interval given as a percent:

`24.4\% \leq p \leq 32.6\%`

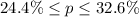
If we express this in terms of fraction we have this:

`0.244 \leq p \leq 0.326`

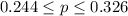
We know that the confidence interval for the true proportion is given by:

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

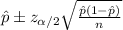
And thats equivalent to:

`\hat p \pm ME`

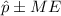
We can estimate the estimated proportion like this:

`\hat p = (0.244+0.326)/(2)=0.285`

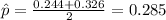
And the margin of error can be estimaed using the fact that the confidence interval is symmetrical

`ME = (0.326-0.244)/(2)=0.041`

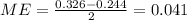
And then the confidence interval in the form desired is:

`0.285 \pm 0.041`