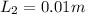Answer:
The length of the side of the hole in the second cardboard sheet is
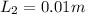
Step-by-step explanation:
From the question we are told that
The distance of the point source from the screen is
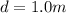
The length of a side of the first square hole is
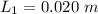
The distance of the cardboard from the point source is

The distance of the second cardboard from the point source is
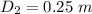
Let take the
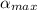 as the angle at which the light is passing through the edges of the cardboards square hole
as the angle at which the light is passing through the edges of the cardboards square hole
Since the bright square casted on the screen by both square holes on the individual cardboards are then it means that
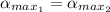
This implies that

Looking at this from the SOHCAHTOA concept

Here opposite is the length of the side of the first cardboard square hole
and
Adjacent is the distance of the from the first cardboard square hole to the point source
And for
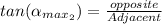
Here opposite is the length of the side of the second cardboards square hole (let denote it with
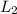 )
)
and
Adjacent is the distance of the from the second cardboards square hole to the point source
So
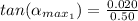
And
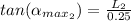
Substituting this into the above equation
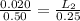
Making
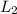 the subject
the subject
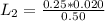
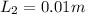
Since it is a square hole the sides are the same hence
The length of the side of the hole in the second cardboard sheet is