Answer:


And in order to obtain the confidence interval for the deviation we just take the square root and we got:
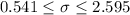
Since the confidence interval cointains the 1 we don't have enough evidence to reject the hypothesis given by the claim
Explanation:
Data provided
1.9, 2.4, 3.0, 3.5, and 4.2
We can calculate the sample mean and deviation from this data with these formulas:

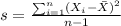
And we got:

s=0.903 represent the sample standard deviation
n=5 the sample size
Confidence=95% or 0.95
Confidence interval
We need to begin finding the confidence interval for the population variance is given by:

The degrees of freedom given by:

The Confidence level provided is 0.95 or 95%, the significance is then
 and
and
 , and the critical values for this case are:
, and the critical values for this case are:
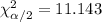
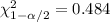
And the confidence interval would be:


And in order to obtain the confidence interval for the deviation we just take the square root and we got:
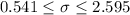
Since the confidence interval cointains the 1 we don't have enough evidence to reject the hypothesis given by the claim