Question

A college entrance exam company determined that a score of 2323 on the mathematics portion of the exam suggests that a student is ready for​ college-level mathematics. To achieve this​ goal, the company recommends that students take a core curriculum of math courses in high school. Suppose a random sample of 150150 students who completed this core set of courses results in a mean math score of 23.423.4 on the college entrance exam with a standard deviation of 3.23.2. Do these results suggest that students who complete the core curriculum are ready for​ college-level mathematics? That​ is, are they scoring above 2323 on the math portion of the​ exam? Complete parts​ a) through​ d) below.

Answer 1

a) The null and alternative hypothesis are:

`H_0: \mu=23\\\\H_a:\mu> 23`

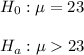
c) Test statistic t=1.53

P-value=0.064

d) The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that students who complete the core curriculum are ready for​ college-level mathematics. That is that the true score for the group is not significantly higher than 23.

Explanation:

The question is incomplete:

a) State the appropriate null and alternative hypotheses.

c) Use the P-value approach at the 0.05 level of significance to test the hypotheses in part (a). ldentify the test statistic. (Round to two decimal places as needed.) Identfy the P-value. P-value (Round to three decimal places as needed.)

d) Write a conclusion based on the results. Choose the correct answer below. ? the null hypothesis and claim that there ? sufficient evidence to conclude that the population mean is ? than 20.

This is a hypothesis test for the population mean.

The claim is that students who complete the core curriculum are ready for​ college-level mathematics.

Then, the null and alternative hypothesis are:

`H_0: \mu=23\\\\H_a:\mu> 23`

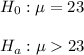
The significance level is assumed to be 0.05.

The sample has a size n=150.

The sample mean is M=23.4.

As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=3.2.

The estimated standard error of the mean is computed using the formula:

`s_M=(s)/(√(n))=(3.2)/(√(150))=0.261`

Then, we can calculate the t-statistic as:

`t=(M-\mu)/(s/√(n))=(23.4-23)/(0.261)=(0.4)/(0.261)=1.531`

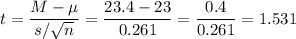
The degrees of freedom for this sample size are:

`df=n-1=150-1=149`

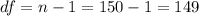
This test is a right-tailed test, with 149 degrees of freedom and t=1.531, so the P-value for this test is calculated as (using a t-table):

`P-value=P(t>1.531)=0.064`

As the P-value (0.064) is bigger than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that students who complete the core curriculum are ready for​ college-level mathematics.