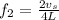Question

A simple experiment to measure the speed of sound doesn't involve a stopwatch. You can fill up along tube with water and put a tuning fork over the opening. The sound waves that travel down into the tube will reflect from the surface of the water and come back to the tuning fork. This is like a half open pipe with a fixed end condition on the water side and an open end condition on the openThe condition for resonance is if the depth of the air column is an odd integer multiple of lamda/4. The speed of sound is 345 m/s.A) If a tuning fork was used for this experiment, what is the depth of the air column that will satisfy the resonance condition for the fundamental mode?B) What is the depth of L3the air column for the 3rd harmonic resonance?C) Is there a depth that will result in a 2nd harmonic resonance? Explain

Answer 1

Step-by-step explanation:

In order to answer this problem you have to know the depth of the column, we say R, this information is important because allows you to compute some harmonic of the tube. With this information you can compute the depth of the colum of air, by taking tino account that the new depth is R-L.

To find the fundamental mode you use:

`f_n=(nv_s)/(4L)`

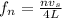
n: mode of the sound

vs: sound speed

L: length of the column of air in the tube.

A) The fundamental mode id obtained for n=1:

`f_1=(v_s)/(4L)`

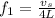
B) For the 3rd harmonic you have:

`f_3=(3v_s)/(4L)`

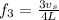
C) For the 2nd harmonic:

`f_2=(2v_s)/(4L)`