Question

According to the National Institute on Drug Abuse, a U.S. government agency, 17.3% of 8th graders in 2010 had used marijuana at some point in their lives. A school official hopes to show the percentage is lower in his district, testing LaTeX: H_0H 0: LaTeX: p=0.173p = 0.173 versus LaTeX: H_aH a: LaTeX: p<0.173p < 0.173. The health department for the district uses anonymous random sampling and finds that 10% of 80 eighth-graders surveyed had used marijuana. Are conditions met for use of the normal model to represent the distribution of sample proportions?

Answer 1

The conditions for use of the normal model to represent the distribution of sample proportion are not met. He should increase the sample size until the conditions are met.

If the test is done anyway, the null hypothesis failed to be rejected.

The conclusion is taht there is not enough evidence to support the claim that the percentage is lower in this district.

Explanation:

The conditions for use of the normal model to represent the distribution of sample proportion are not met, as the affirmative responses are less than 10.

`np=80*0.1=8<10`

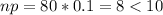
If the test of hypothesis is done as if the conditiones were met, we know that the claim is that the percentage is lower in this district.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.173\\\\H_a:\pi<0.173`

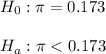
The significance level is 0.05.

The sample has a size n=80.

The sample proportion is p=0.1.

The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.173*0.827)/(80)}\\\\\\ \sigma_p=√(0.001788)=0.042`

Then, we can calculate the z-statistic as:

`z=(p-\pi+0.5/n)/(\sigma_p)=(0.1-0.173+0.5/80)/(0.042)=(-0.067)/(0.042)=-1.578`

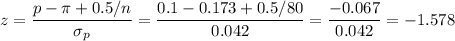
This test is a left-tailed test, so the P-value for this test is calculated as:

`P-value=P(z<-1.578)=0.057`

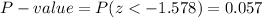
As the P-value (0.057) is greater than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the percentage is lower in this district.